移動平均法|工程管理・計画

移動平均法は、過去データの平均を算出し、導き出した数値を予測値とする考え方です。
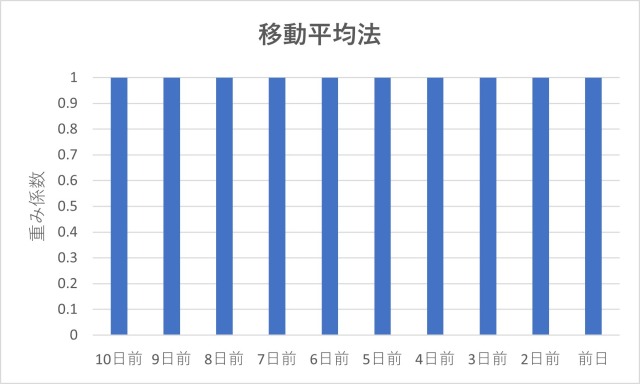
データの重みづけが時期によらず均等で、過去のデータも直近のデータも同等に扱います。
考え方や計算式がシンプルなため、扱いやすい手法です。

移動平均法の特徴

移動平均法には、次のような特徴があります。

・偶然性に起因する需要変動（ノイズ）を取り除いて予測できる
・需要の変化（傾向・周期）への対応が遅れる
・需要変動の傾向成分、周期成分を抽出できる

算出が簡単なため、市場の変化や仕入額の変動など何かしらの変化があるたびに計算すればよいので、変化に対して柔軟に対応できます。一方で、変化が多くなると計算を行う回数が多くなるため、担当者の負担は大きくなります。

10日間を例にとった重み係数の推移は次のようになります。

移動平均法は、時系列データの変動を平滑化するための手法で、データのトレンドや季節性を把握するのに役立ちます。この手法は、過去のデータポイントの平均を計算し、その結果を新しいデータと組み合わせて予測を行います。

単純移動平均 (SMA)
一定期間のデータの単純な平均を計算します。たとえば、5日間のデータの平均を計算する場合、直近5日間の値を合計し、5で割ります。
$$\text{SMA} = \frac{X_1 + X_2 + X_3 + X_4 + X_5}{5}$$
加重移動平均 (WMA)
各データポイントに異なる重みを付けて平均を計算します。一般的に、最近のデータに対して大きな重みを付け、過去のデータには小さな重みを付けます。
$$\text{WMA} = \frac{w_1X_1 + w_2X_2 + w_3X_3 + w_4X_4 + w_5X_5}{w_1 + w_2 + w_3 + w_4 + w_5}$$
指数平滑法 (EWMA
過去のデータに指数的に減少する重みを付けて平均を計算します。これは、最近のデータにより多くの重みを与え、古いデータには少ない重みを与えます。
$$S_t = \alpha X_t + (1 – \alpha) S_{t-1}$$
ここで、$ S_t$ は時点 $ t $ の予測値、$ \alpha $ は平滑化係数 (0 < α < 1)、$ X_t $ は時点 $ t $ の実績値です。

遅れの発生: 移動平均法は過去のデータに基づいて計算されるため、特に急激な変化やトレンドの転換に対して反応が遅れる可能性があります。
データの選択: 移動平均の期間（例えば、5日、10日、30日など）を選択する際には、データの性質や分析目的を考慮する必要があります。
季節性の影響: データに季節性がある場合、単純な移動平均だけでは十分にトレンドを把握できないことがあります。この場合は、季節調整を行ったり、季節的移動平均法を用いることが推奨されます。