加重移動平均法 |工程管理・計画

加重移動平均法（Weighted Moving Average, WMA）は、時系列データの分析手法の一つで、データの最近の値により大きな重みを与えつつ、過去の値も考慮して平均を計算します。これにより、最近の変動がより反映されやすくなり、データのトレンドやパターンをより正確に把握することができます。

重み係数

各データに異なる係数を掛けることで求めます。
一定期間内のデータを使用し、その間の重み係数は等間隔 (例えば 0.1 刻み、0.5刻み)に変動させます。
移動平均法の一種で、古い需要の影響を少なくし、最新の需用変動の影響を多く取り入れる考え方です。

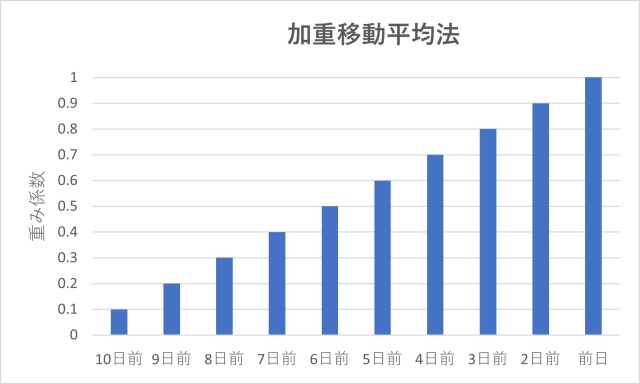
10日間を例にとり、重み係数を0.1刻みとした場合の、重み係数の推移は次のようになります。

概要

加重移動平均法は、特定の期間におけるデータの値に異なる重みを付けて平均を計算することで、過去のデータの影響を調整します。一般的に、最近のデータに高い重みを与え、古いデータの重みを徐々に減少させることが特徴です。

目的

トレンドの把握: データのトレンドやパターンを明確にし、予測や分析を行うための基盤を提供します。
ノイズの低減: 短期的な変動やノイズを平滑化し、より信頼性のある情報を抽出します。

方法

加重移動平均法の計算手順は以下の通りです。

重みの設定: 分析したい期間（n）の各データに対して、重みを設定します。通常、最近のデータに高い重みを、古いデータに低い重みを与えます。
計算: 各データに重みを掛け、その合計を重みの合計で割ります。計算式は以下のようになります。$$WMA = \frac{(w_1 \times x_1) + (w_2 \times x_2) + … + (w_n \times x_n)}{w_1 + w_2 + … + w_n}$$
ここで、$x_i $は各データポイント、$w_i$ はそのデータポイントに対応する重みです。

事例

例えば、過去5日間の株価を考えた場合、最近の3日間のデータに対して高い重みを与え、古い2日間には低い重みを与えるとします。

日1: 株価 100（重み 1）
日2: 株価 102（重み 2）
日3: 株価 105（重み 3）
日4: 株価 103（重み 2）
日5: 株価 101（重み 1）

この場合、WMAは次のように計算されます。

\begin{align}WMA &= \frac{(100 \times 1) + (102 \times 2) + (105 \times 3) + (103 \times 2) + (101 \times 1)}{1 + 2 + 3 + 2 + 1}\\&= \frac{100 + 204 + 315 + 206 + 101}{9} \\&= \frac{926}{9} \approx 102.89\end{align}