ここでは、技術士総合技術監理試験で定期的に出題される、
割引率(年利率)を使用する計算問題の解き方について説明いたします。
割引率の詳細な説明はこちら
割引率を使用した事業投資評価手法の説明はこちら
総監試験で出題される、割引率を使用する計算問題は大きく、
1. 複数案件から最適な投資先を選択 R2
2. 買取とリースで比較 H26, R1
3. ある投資案件の資金回収 H25, H28, H30
の３つに分けられます。
いずれの問題も、
将来価値を現在価値に揃えて比較する
という作業を丁寧に行うことで、必ず解くことができます。
手順は、
将来価値を割引率で割ることで、現在価値に換算する
です。
ここまでは、「割引率」「現在価値」「将来価値」の定義に関する内容です。
この概念を覚えておきましょう。
ここまで理解していれば、ほとんどの問題は解けます。
しかし、注意しなければならない点が１つだけあります。それは、
「初」と「末」の違いを意識する
です。「3年」を例にとると、
「3年目初」と「3年目末」では、1年の隔たりがあり、割引率分だけ価値に違いが生じる
ということです。
問題文を読み、横軸に時間、縦軸に価値(プラス側が利益、マイナス側が支出)をとって、毎年の収支を図式化します。
その際、「初」「末」の違いを意識するために、「1年」に幅を持たせて「線」で捉えて図式化して考えます。
簡単な例題
簡単な例題で考えてみましょう。
3年目と8年目の初に100万円受け取る。割引率rを10%とする。このときの現在価値Iを求めよ。
点で捉えた場合
３と8 という点のみ(「初」を考慮しない)に着目して図式化すると、このようになります。
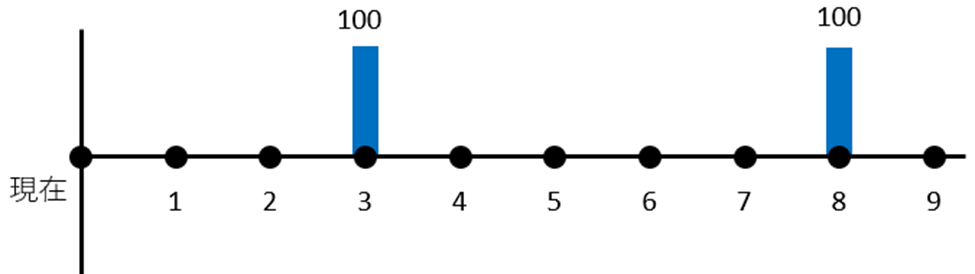
これより、
I = 100÷ (1.1)3 + 100÷ (1.1)8
= 122万円 ①
線で捉えた場合
この場合を図式化すると、このようになります。
両方とも「初」なので3年目の最初の点に１００万円を記します。
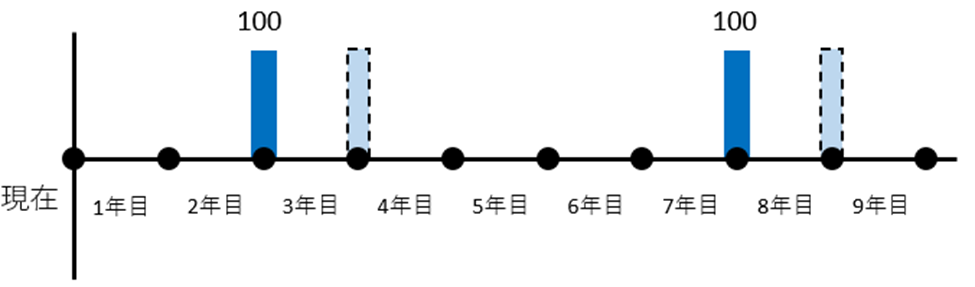
「点で捉えた場合」と比較すると、一つ左にシフトしていることがわかります。
現在価値は、次の通り求まります。
I = 100÷ (1.1)2 + 100÷ (1.1)7
= 134万円 ②
①と②では、割引率１年分の差異が生じます。
解き方のまとめ
将来価値を割引率で割り、現在価値に換算する
「初」「末」を区別して図式化する
この2点を実行するだけで総監択一問題で出題される問題は解けます。
関数電卓の持ち込みはできないので、電卓へのインプットミスが生じる可能性があります。
立式した後、両辺に (1+r)n をかけることで式が簡単になる場合があるので、立式までは丁寧に行い、簡略化できないかを考えるとよいでしょう。
総監択一問題 過去問
実際に出題された問題を解いてみましょう。
