ある会社では、ある機械の設備投資に際して、買取りにするかリースにするかについて検討している。
以下に示す条件において、リースによる場合の総費用の現在価値が、買取りによる場合の総費用の現在価値に最も近くなる毎年のリース費用は次のうちどれか。
[条件]
a.考慮する期間:5 年
b.割引率(年利率):10%
c.買取りの場合:
1 年目の初めに1,000 万円を支払い、 5 年目の末に残存価額100 万円で買い戻してもらえる。
なお、設置費用及び撤去費用は無料とする。
d.リースの場合:
5 年間、毎年の初めにリース費用を均等に支払う。
さらに、 1 年目の初めに設置費用として50 万円、また5 年目の末に撤去費用として20 万円をそれぞれ支払う。
e.上で述べたもの以外の費用や収益は考えない。
① 165 万円
② 190 万円
③ 210 万円
④ 225 万円
⑤ 230 万円
【正解③】
この問題は、DCF法(Discounted Cash Flow、割引キャッシュ・フロー)の計算方法の理解について問われています。
理解さえしていれば、ただの算数問題です。
割引率に関する説明はこちら

買取の場合と、リースの場合、それぞれを図式化して問題文の要求を整理します。
ポイントは、
です。
これさえ意識して正しく図式化すれば簡単に解けます。
買取の場合
「万円」を省略して図式化するとこのようになります。
出費を下矢印、収入を上矢印で表します。

図式化するときのポイントは、
「1年」を点ではなく、線(幅)であらわす
です。
そうすることで、「初」と「末」を把握しやすくなります。
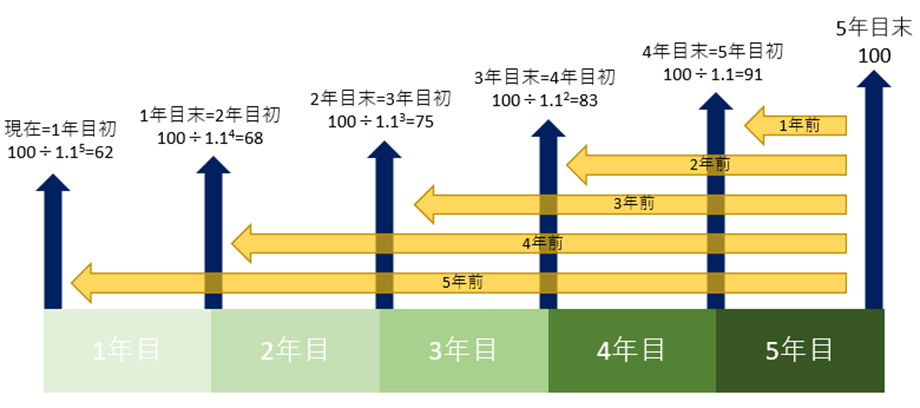
次に、買い戻し収入100(万円)を現在価値に換算します。
「100」のみに着目し、割引率を使用して価値を割り引くと、次の図のようになります。
1年経るごとに、まさに指数関数的に減少することがわかります。
そして、「5年目末の100万円」の現在価値は62万円と求まります。
この結果を最初の図に反映すると、このようになります。
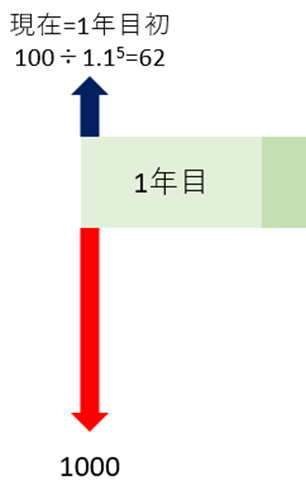
これより、買取の場合の現在価値は、
-1000 + 62 = -938 (万円)
と求まりました。
リースの場合
同様に、リースの場合も図式化すると、次のように表せます。
未知のリース費用をXで表しました。
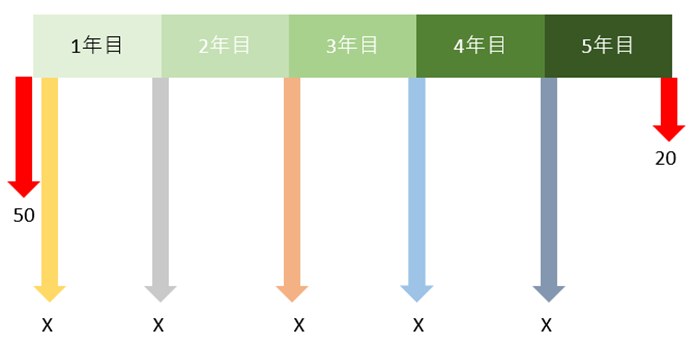
次に、リース費用(5年分のX)と撤去費用20を現在価値に換算します。
「現在」という点を拡大したものが次の図になります。
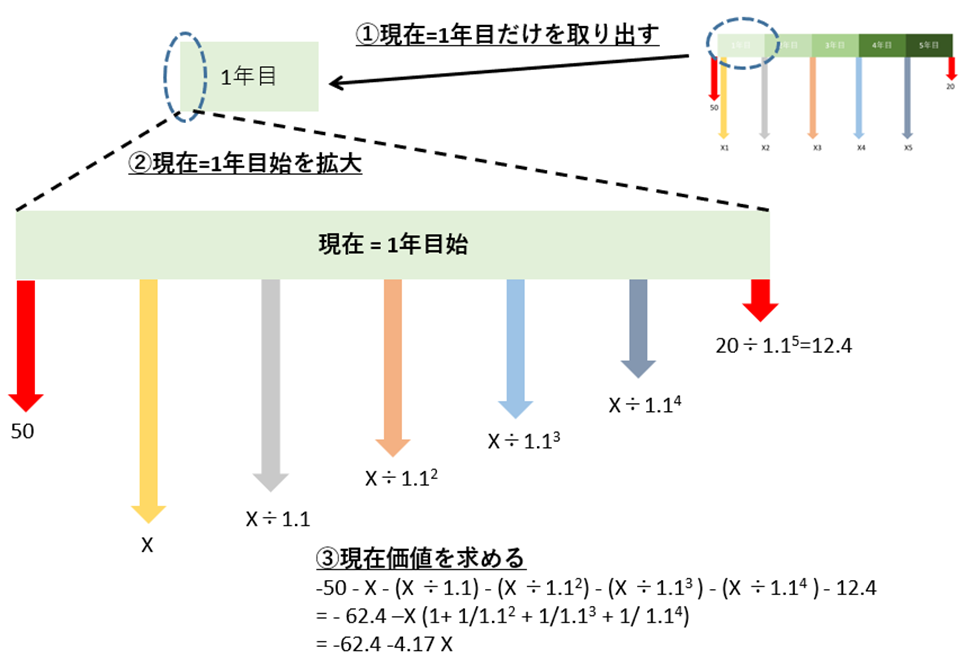
これより、リースの場合の現在価値は、
-50 – X – (X ÷1.1) – (X ÷1.12) – (X ÷1.13 ) – (X ÷1.14 )- 12.4
= – 62.4 –X (1+ 1/1.12 + 1/1.13 + 1/ 1.14)
= -62.4 -4.17 X
と求まります。
買取の場合と同価値になるリース額
買取の場合と、リースの場合の現在価値が等しくなるときのXを求めます。
-938 = -62.4 -4.17 X
⇔ X = 209.98 (万円)
よって、③の210万円が正解となります。









コメント