前工程である工程1 と後工程である工程2 の2 つの工程からなる生産システムがある。
工程1 は設備A 又は設備B のどちらか一方で行われ、工程2 は設備C で行われる。
設備A~C は稼働中に不適合品を発生させないものとし、故障等による設備の停止は互いに独立な事象であるとする。
設備A、設備B の信頼度が、それぞれ、0.950、0.900 であるとき、システム全体の信頼度が0.900 を超えるために最低限必要な設備C の信頼度に最も近い値はどれか。
ただし、 効数字は3 桁で計算せよ。
① 0.804
② 0.851
③ 0.905
④ 0.947
⑤ 0.973
【正解③】
システム信頼性の問題の解き方はこちら
あわせて読みたい


【システム信頼性】の考え方と解き方
技術士一次試験、技術士総合技術監理試験で、システム信頼性は頻出問題です。ここでは、システム信頼性の考え方について説明いたします。 信頼度(信頼性)をR (Reliabili...
この全行程を図式化すると、下図のように表せます。
ここでRを信頼度、Eを故障率と置き、R+E=1が成り立ちます。
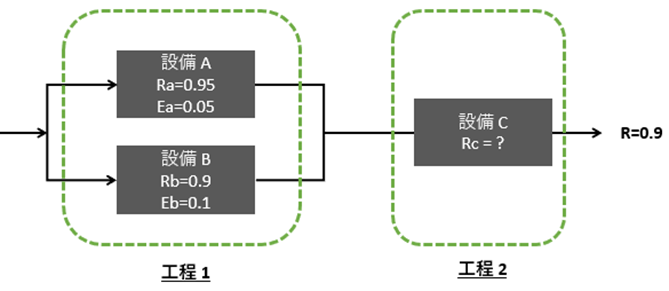
次に、並列関係にある工程1の信頼性を求めます。
工程1の信頼性は、故障率の余事象と考えます。
すると、R1 = 1 – Ea×Eb と求まります。
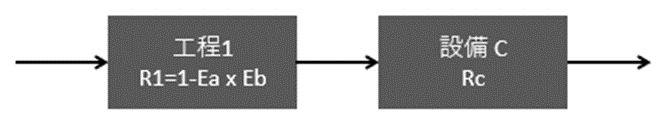
次に、直列関係にある工程1と設備Cの信頼性、つまり全体の信頼性を求めます。
要素が直列関係にある信頼性は、それぞれの信頼性の積で求まります。
よって、
R = R1 × Rc
= (1 – Ea×Eb) ×Rc

R>0.900 となるのは、
(1 – Ea×Eb) ×Rc > 0.900
⇔ (1 – 0.05×0.1) ×Rc > 0.900
⇔ Rc > 0.9045
と求まります。
よって、③が最も近い解答となります。









コメント