試験を行ったところ、得点の度数分布は下表のようになった。この得点分布の平均値、中央値、第3 四分位数の大小関係として、次のうち最も適切なものはどれか。
表 得点の度数分布
| 得点 | 人数 | 累積人数 |
|---|---|---|
| 0点以上9点以下 | 2 | 2 |
| 10点以上19点以下 | 7 | 9 |
| 20点以上29点以下 | 9 | 18 |
| 30点以上39点以下 | 10 | 28 |
| 40点以上49点以下 | 13 | 41 |
| 50点以上59点以下 | 14 | 55 |
| 60点以上69点以下 | 19 | 74 |
| 70点以上79点以下 | 21 | 95 |
| 80点以上89点以下 | 51 | 146 |
| 90点以上100点以下 | 4 | 150 |
① 平均値＜中央値＜第3 四分位数
② 第3 四分位数＜中央値＜平均値
③ 中央値＜平均値＜第3 四分位数
④ 第3 四分位数＜平均値＜中央値
⑤ 表の情報だけからでは大小関係が一意に決まらない
【正解①】
平均値、中央値、第3四分位数の定義を覚えていれば簡単に解ける問題です。 中央値と第3四分位数の定義は、
データを小さい順に並べて、下から1/4のところのデータを第1四分位数、2/4のところのデータを第2四分位数（中央値と同じ）、3/4のところのデータを第3四分位数
です。これをイメージ化すると、下の図のようになります。 最も小さい値を最小、最も大きな値を最大とおくと、最小をとる値から1/4のところが第1四分位数、中央が第2四分位数、3/4のところが第３四分位数です。
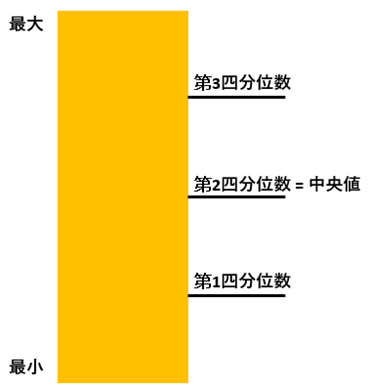
本問題では、中央値と第3四分位数は累積人数を確認することで求めることができます。
