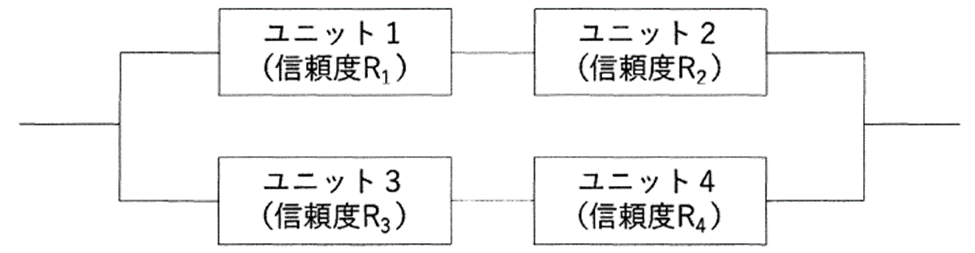
下図のシステムにおいて、ユニット1 から3 の信頼度はR1=R2=R3=0.9 である。
ユニット4の信頼度として次の値が選べるとき、システム全体の信頼度を0.9 以上とする要求を満たす最小の値はどれか。
ただし、各ユニットの故障発生は独立事象とする。
① 0.5
② 0.6
③ 0.7
④ 0.8
⑤ 0.9
【解答②】
この問題のシステムを2段階のステップで単純化し、解を導き出します。
詳細はこの記事をお読みください。
あわせて読みたい


【システム信頼性】の考え方と解き方
技術士一次試験、技術士総合技術監理試験で、システム信頼性は頻出問題です。ここでは、システム信頼性の考え方について説明いたします。 信頼度(信頼性)をR (Reliabili...
STEP
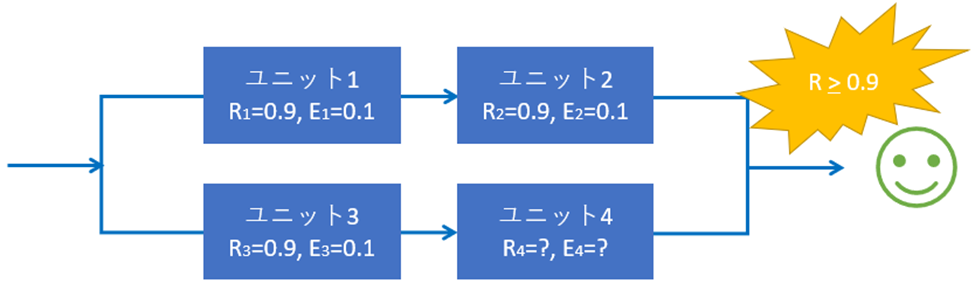
システムに、ユニットの信頼度と故障率を記入する
STEP
ユニット1 とユニット2、ユニット3とユニット4を直列の関係を用いて、信頼度と故障率を求める。
信頼度 R1&2 = R1 × R2 = 0.81
R3&4 = 0.9 × R4 = 0.9・R4
故障率 E1&2 = 1- R1&2 = 0.19
E3&4 = 1-R3&4 = 1-0.9・R4
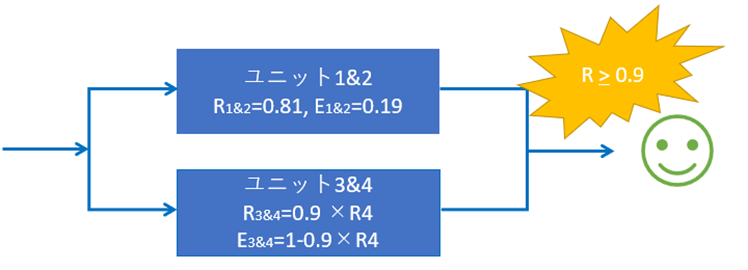
ここで、故障率の導出には余事象の関係を用いた。
STEP
ユニット1 とユニット2、ユニット3とユニット4を直列の関係を用いて、信頼度と故障率を求める。
ユニット1&2 とユニット3&4 を、並列の関係を用いて、システム全体の信頼度と故障率を求める。
故障率 E = E1&2×E3&4
= 0.19 ×(1-0.9・R4)
信頼度 R =1- E
= 1-{0.19 ×(1-0.9・R4)}
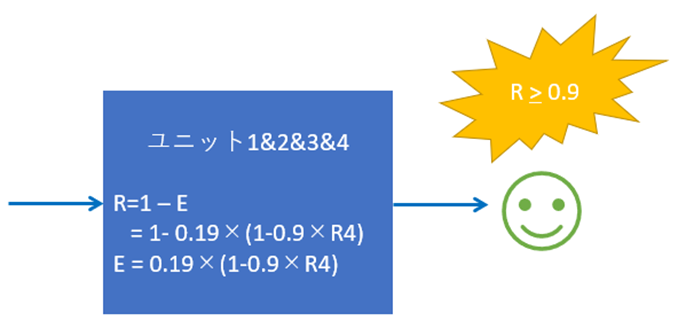
最後に、信頼度R が0.9以上となる不等式を解き、R4を求める。
R > 1-{0.19 ×(1-0.9・R4)}
⇔0.9 > 1-{0.19 ×(1-0.9・R4)}
⇔ R4 > 0.526
つまり、ユニット4の信頼度が0.527以上であればシステム全体の信頼度は0.9以上となる。









コメント