現在価値、年価、終価は、資金の時間価値を考慮するための重要な概念です。
それぞれの定義、計算方法、具体例を以下に説明します。
現在価値 (Present Value: PV)
現在価値は、将来受け取るキャッシュフローを、特定の利率で現在の価値に割り引いたものです。将来の価値を現在の価値に換算することで、投資の価値を評価します。
計算式
現在価値の計算は以下の式を用います。$$PV = \frac{FV}{(1 + r)^n}$$
- PV: 現在価値
- FV: 将来価値
- r: 割引率(利率)
- n: 将来の期間(年数)
具体例
例えば、3年後に100,000円を受け取るとします。割引率が5%の場合、現在価値は以下のように計算されます。
$$PV = \frac{100,000}{(1 + 0.05)^3} \approx \frac{100,000}{1.157625} \approx 86,383.76 \text{円}$$
この場合、現在価値は約86,384円です。
年価 (Annual Worth: AW)
年価は、特定の期間内における資金の年単位の価値を示す指標で、資産の評価や投資の比較に利用されます。将来のキャッシュフローを年単位で均等に分配した価値を表します。
計算式
年価は、現在価値または将来価値を基に以下の式で計算されます。
$$AW = \frac{PV \times r \times (1 + r)^n}{(1 + r)^n – 1}$$
または
$$AW = \frac{FV \times r}{(1 + r)^n – 1}$$
具体例
上記の現在価値の例を用いて、割引率が5%、期間が3年の場合、年価を計算します。
まず、現在価値が86,384円だったので、年価は次のように計算されます。
$$AW = \frac{86,383.76 \times 0.05 \times (1 + 0.05)^3}{(1 + 0.05)^3 – 1}$$
計算すると、
$$AW \approx 30,000 \text{円}$$
この場合、年価は約30,000円となります。
終価 (Future Value: FV)
終価は、現在投資した資金が、特定の利率で成長した結果、将来的に得られる金額を示します。投資が時間とともにどのように成長するかを評価します。
計算式
終価の計算は以下の式を用います。
$$FV = PV \times (1 + r)^n$$
- FV: 終価
- PV: 現在価値
- r: 利率
- n: 期間(年数)
具体例
例えば、現在50,000円を投資し、年利率が5%で5年間運用するとします。終価は以下のように計算されます。
$$FV = 50,000 \times (1 + 0.05)^5 \approx 50,000 \times 1.276281 \approx 63,814.05 \text{円}$$
この場合、終価は約63,814円です。
まとめ
- 現在価値 (PV)は、将来のキャッシュフローを現在の価値に割り引いたもので、投資の価値を評価する際に使用されます。
- 年価 (AW)は、特定の期間内における年単位の資金価値を示し、資産の評価や投資の比較に利用されます。
- 終価 (FV)は、現在の投資が将来的に成長した結果得られる金額で、投資の将来的な価値を評価します。
これらの概念を理解することで、資金運用や投資の意思決定においてより良い判断ができるようになります。
6つの係数をまとめると次のようになります。いずれも複利運用を想定しています。
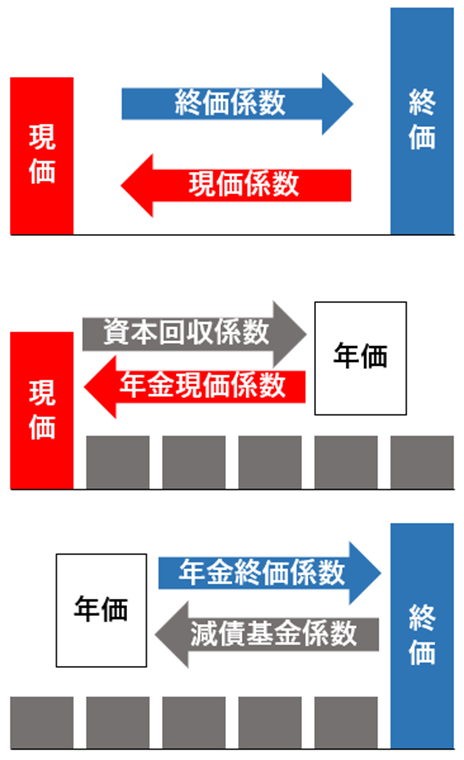
| 終価係数 | 現価(PV)から終価(FV) | 現在投資し、将来受け取る額(FV) |
| 現価係数 | 終価(FV )から現価(PV ) | 将来、受け取るために、現在いくら投資しなければない額 |
| 資本回収係数 | 現価(PV)から年価(AW ) | 現在PVあり、ある期間中毎年定額を取り崩すさい、受けれる額AW |
| 年金現価係数 | 年価(AW )から現価(PV) | ある期間同額AWを受け取るため、現在準備しなければならない額PV |
| 減債基金係数 | 終価(FV )から年価(AW ) | 将来FV受け取るために、毎年の積立額AW |
| 年金終価係数 | 年価(AW)から終価(FV ) | 毎年の積立AWで、将来受け取る額FV |









コメント