技術士一次試験、技術士総合技術監理試験で、システム信頼性は頻出問題です。
ここでは、システム信頼性の考え方について説明いたします。
信頼度(信頼性)をR (Reliability の頭文字)、故障率 をE (Error Ratio の頭文字)で表します。
このとき、
R + E =1
が成り立ちます。
そして、ある独立した要素をSとすると、入力と出力は次のように図式化できます。

「正常に出力される確率がR」、「正常に出力されない確率がE」と言えます。
次に、要素が2つある場合を考えます。
2つの要素を S1、S2とし、それぞれの信頼度と故障率を R1、R2、E1、E2と一般化して考えます。
そして、全体の信頼度と故障率を R、Eと置きます。
要素が2つある場合、要素の並び方には直列と並列の2通りがあります。
それぞれを図式化すると、次のように表せます。
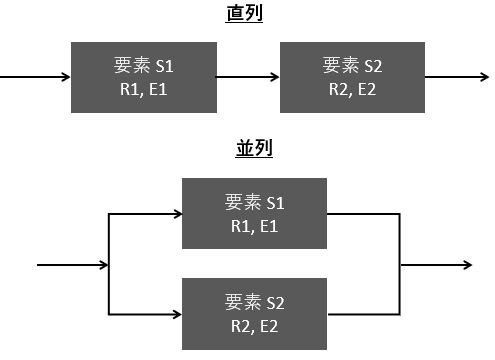
つぎに、それぞれの場合における全体の信頼度と故障率を考えます。
直列の場合
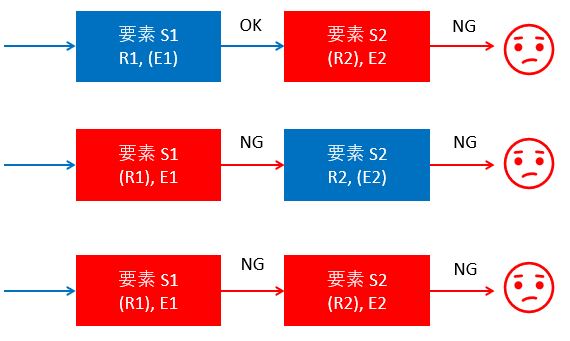
2つの要素両方ともが正常であればシステム全体も正常です。
言い換えると、1つの要素でも故障していると、システム全体も「故障」状態となります。
これより、全体信頼度Rと全体故障率Eは次のように求めることができます。
直列の場合の全体信頼度
R = (S1正常 & S2正常)
= R1・R2 ①

直列の場合の全体故障率
E = (S1故障 & S2故障) + (S1正常 & S2故障) +(S1故障 & S2正常)
= E1・E2 + R1・E2 + E1・R2 ②
また、R + E=1 の関係より、
E = 1-R
= 1 – R1・R2 ③
= 1- (1 – E1) ・(1 – E2) ④
と表すこともできます。
信頼度と故障率の合計
R + E = ①+②
=(R1・R2) + (E1・E2 + R1・E2 + E1・R2)
= (R1 + E1)・(R2 + E2) ⑤
= 1 x 1
= 1
並列の場合
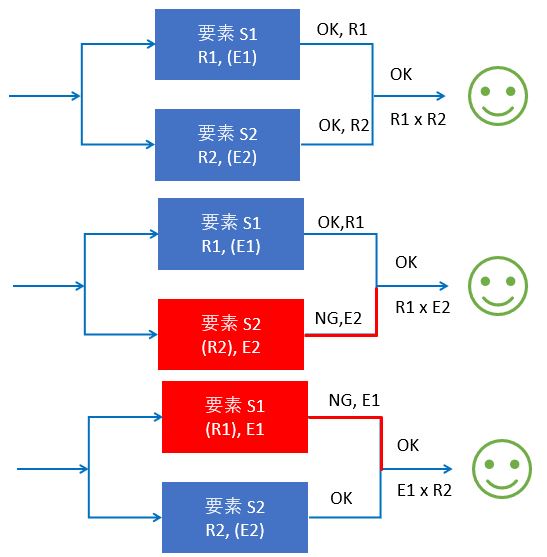
2つの要素両方ともが故障していると、システム全体も「故障」状態となります。
言い換えると、1つの要素でも正常であれば、システム全体も正常状態を維持できます。
これより、全体信頼度Rと全体故障率Eは次のように求めることができます。
並列の場合の全体故障率
E = (S1故障 & S2故障)
= E1・E2 ⑥

並列の場合の全体信頼度
R = (S1正常 & S2正常) + (S1正常 & S2故障) +(S1故障 & S2正常)
= R1・R2 + R1・E2 + E1・R2 ⑦
また、R + E=1 の関係より、
R = 1-E
= 1 – E1・E2 ⑧
= 1- (1 – R1) ・(1 – R2) ⑨
と表すこともできます。
信頼度と故障率の合計
R + E = ⑥+⑦
= (E1・E2) + (R1・R2 + R1・E2 + E1・R2)
= (R1 + E1)・(R2 + E2) ⑩
= 1 x 1
= 1
図でとらえる
直列、並列ともに、信頼度と故障率の合計は、
R + E = (R1 + E1)・(R2 + E2) ⑤⑩
という式で表されます。
これは、1 x 1 の正方形と考えることができます。
この関係を図式化すると次のようになります。
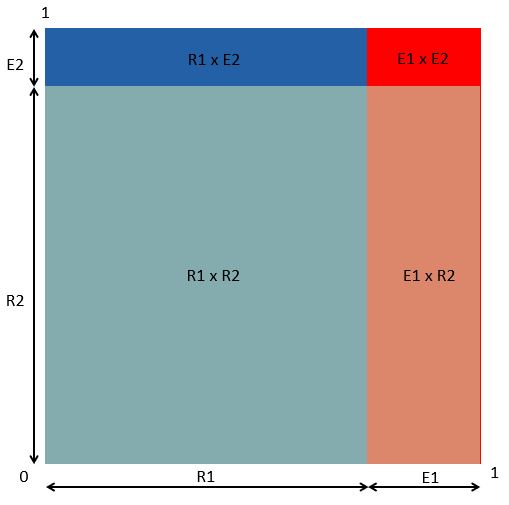
次に、この図を使用して信頼度と故障率を考えてみます。
図で考える、直列の場合の全体信頼度
両方が正常 = 「Rのみの項」が対象
よって、 R = R1 x R2
図で考える、直列の場合の全体故障率
一つ以上の要素が故障している = 一つ以上Eが含まれている項が対象
よって、E = E1・E2 + R1・E2 + E1・R2
図で考える、並列の場合の全体信頼度
一つ以上の要素が正常 = 一つ以上Rが含まれている項が対象
よって、 R = R1・R2 + R1・E2 + E1・R2
図で考える、並列の場合の全体故障率
両方の要素が故障している = 「Eのみが含まれている項」が対象
よって、E = E1 x E2
考察
- 直列・並列ともに、信頼度にR1 x R2が含まれる。
- 直列・並列ともに、故障率にE1 x E2が含まれる。
- 直列と並列の違いは、信頼度Eと故障率Rの両方を含む項である「R1・E2 + E1・R2」を信頼度と故障率のどちらに含めるのかの違いである。
3つ以上の要素から構成される場合
3つ以上の要素から構成される場合、上記で考えた2つの要素の信頼度と故障率を求めることで、1つの要素として扱うことで要素数を減らすことができます。
この作業を繰り返すことで、全体の信頼度と故障率を求めることができます。
技術士 総監択一問題
技術士試験 総合技術管理部門 択一問題で出題された問題を解いてみましょう。








コメント